This is the fourth in a multi-part series showing how statistical techniques can make your loan quality control more efficient and more effective.
4 – Use One-Sided Confidence Intervals, Not Two-Sided
PRINCIPLE
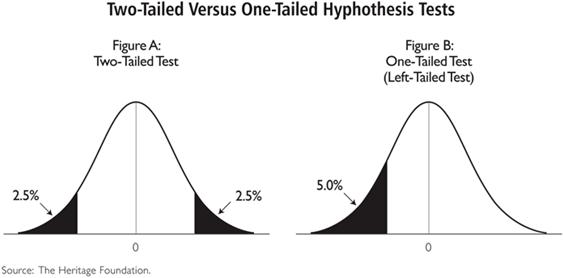
In mortgage quality control, our risk lies only in underestimating the number of defective loans. We seek to make the statement that “we are 95% confident that our defect rates are no worse than X%”. We do not need to state that the defect rate is between X% and Y%. Therefore, we can use a one-sided confidence interval (or “one-tailed test”), which requires a smaller sample size than a two-sided confidence interval to achieve the same precision.
ILLUSTRATION
Quality control in manufacturing is often about minimizing variation around a certain tolerance range. For example, if you are a screw manufacturer, you care that your screws are neither too narrow nor too wide. You want to make the statement that “we are 95% sure that the width of our screws is between X and Y.” So for purposes of statistically sampling screws to examine, you would use a two-sided confidence interval to determine your sample size.
In contrast, a mortgage “manufacturer” only cares that their defect rate is no greater than X%. Therefore, a mortgage manufacturer can use a one-sided rather than a two-sided confidence interval. This makes a real difference in workload.
Note that many online statistical calculators default to a two-sided confidence interval, as do some outsourced service providers. Be sure to control your own sampling and ensure you are not over-sampling.
EXAMPLE
In our previous posts, we saw how a lender originating 15,000 loans per year could reduce sample sizes by reducing their defect rate and/or reducing their precision requirement. Using the same example, again with an 8% defect rate, we see can see the effect of using a one-sided vs. a two-sided confidence interval.
Using Cogent’s Statistical Sample Size Calculator, the two-sided confidence interval yields an annual sample size of 675 loans. The one-sided confidence interval yields an annual sample size of 479 loans. Assuming a cost of $200 per audit, this is valued at $39,200 per year.
About Cogent QC Systems
We embed and automate statistical principles throughout our award-winning QC and risk management applications, making you more efficient and more effective at each step of your workflow.